تلفیق هوش مصنوعی و نظریه گراف به زبان ساده

مقدمه

نظریه گراف، شاخه ای جذاب و کاربردی از ریاضیات است که به مطالعه ی گراف ها، یعنی مجموعه هایی از نقاط به نام رئوس (یا گره ها) که توسط خطوط به نام یال ها به یکدیگر متصل می شوند، می پردازد. تاریخچه ی نظریه گراف به قرن هجدهم و مسئله ی هفت پل کونیگسبرگ بازمی گردد، جایی که لئونهارد اویلر برای اولین بار این مسئله را با استفاده از مفاهیم گراف حل کرد و بدین ترتیب بنیان های نظریه گراف را گذاشت.

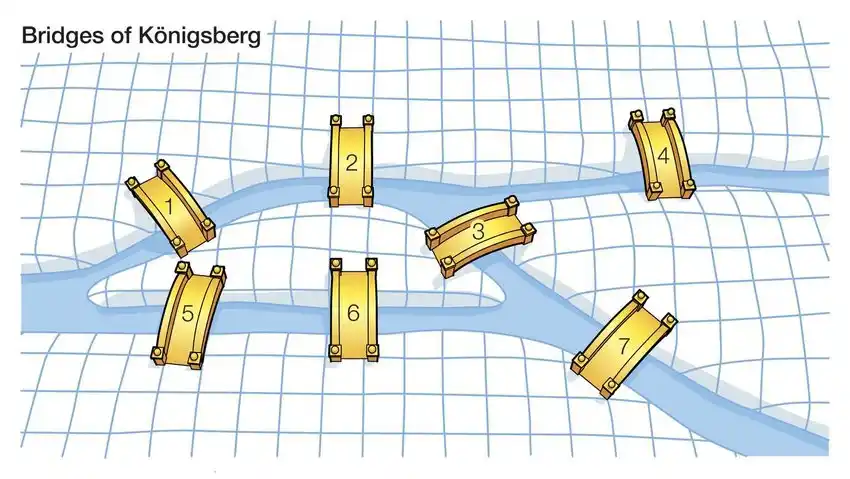
از آن زمان تا کنون، نظریه گراف به ابزاری قدرتمند در بسیاری از زمینه های علمی تبدیل شده است. در علوم کامپیوتر، نظریه گراف برای مدل سازی ساختارهای داده و طراحی الگوریتم های کارآمد به کار می رود. در علم اقتصاد، گراف ها برای تحلیل شبکه های اقتصادی و برنامه ریزی منابع استفاده می شوند. علاوه بر این، در زمینه هایی مانند بیولوژی، جامعه شناسی و حتی در تحلیل شبکه های اجتماعی، کاربردهای نظریه گراف به وضوح قابل مشاهده است.

این شاخه از ریاضیات، با ارائه مفاهیمی مانند مسیر، دور، اتصال و قطعیت، امکان بررسی و فهم بهتر ساختارهای پیچیده ی متصل را فراهم می آورد. مثال های بارزی از این کاربردها می توان به مسیریابی در شبکه های حمل و نقل، برنامه ریزی شهری، و حتی طراحی مدارهای الکترونیکی اشاره کرد. با توجه به پیشرفت های تکنولوژی و افزایش داده های موجود، نقش نظریه گراف در تحلیل و حل مسائل مختلف همچنان در حال گسترش است و پتانسیل های جدیدی را در پیش روی دانشمندان قرار می دهد.

مفاهیم اصلی نظریه گراف

گراف به مجموعه ای از نقاط موسوم به رئوس (یا گره ها) گفته می شود که توسط خطوطی به نام یال ها به یکدیگر متصل هستند. این ساختار ساده در ظاهر، امکان مدل سازی روابط و تعاملات در شبکه های مختلف را فراهم می آورد.

گراف های جهت دار و غیرجهت دار

• گراف غیرجهت دار: در این نوع گراف، یال ها بدون جهت هستند، یعنی تفاوتی بین رفت و برگشت بین دو راس وجود ندارد.
• گراف جهت دار: در گراف های جهت دار، هر یال جهت دار است و جهت یال نشان دهنده ی جهت جریان یا رابطه ی بین دو راس است.

ماتریس همسایگی و لیست همسایگی

• ماتریس همسایگی: یک روش نمایش گراف که در آن رئوس در سطرها و ستون های یک ماتریس قرار دارند و وجود یک یال بین هر دو راس با ۱ و عدم وجود آن با ۰ نشان داده می شود.
• لیست همسایگی: روش دیگری برای نمایش گراف که در آن برای هر راس، لیستی از رئوسی که با آن متصل هستند، ذخیره می شود.

انواع گراف ها

• گراف ساده: گرافی است که نه حلقه دارد و نه یال های موازی.
• مولتی گراف: گرافی که می تواند شامل یال های موازی باشد.
• گراف وزن دار: گرافی که هر یال آن دارای وزن یا ارزش است که معمولا برای نمایش هزینه، زمان یا مقدار منابع بین دو راس به کار می رود.
• گراف کامل: گرافی که هر دو راس آن به طور مستقیم به یکدیگر متصل هستند.

خواص و قضایا در نظریه گراف

قضایا

1. قضیه ی دو رنگی (قضیه ی چرخه های فرد)

• این قضیه بیان می کند که یک گراف ساده بدون چرخه های فرد می تواند فقط با دو رنگ رنگ آمیزی شود، به گونه ای که هیچ دو راس مجاوری همرنگ نباشند. این خاصیت برای بررسی دو بخشی بودن گراف ها استفاده می شود.

2. قضیه ی اویلر

• یک گراف متصل که دارای حداقل دو راس باج دارد، یک مسیر اویلری دارد اگر و تنها اگر دقیقا دو راس دارای درجه فرد باشند. همچنین، یک گراف متصل دارای یک دور اویلری است اگر و تنها اگر همه رئوس آن دارای درجه زوج باشند.

3. قضیه ی همیلتون

• یک گراف دارای یک دور همیلتونی است اگر بتوان آن را طوری دنبال کرد که هر راس دقیقا یک بار بازدید شود و به راس اولیه بازگردد. تعیین اینکه آیا یک گراف دارای دور همیلتونی است یا نه، اغلب چالش برانگیز است و جزو مسائل NP-کامل محسوب می شود.

خواص

1. هم پوشانی و دور

• هم پوشانی (Connectivity): این خاصیت میزان مقاومت یک گراف در برابر قطع شدن را نشان می دهد. یک گراف k-متصل است اگر نیاز به حذف حداقل k راس برای قطع کردن گراف باشد.
• دور (Cycle): یک دور در گراف مسیری است که از یک راس شروع شده و به همان راس باز می گردد بدون آنکه هیچ راسی بیش از یک بار بازدید شود.

2. مسیر

• مسیر در نظریه گراف به دنباله ای از رئوس گفته می شود که هر دو راس متوالی در آن توسط یک یال به هم متصل هستند. مسیر می تواند ساده باشد، به این معنا که هیچ راسی بیش از یک بار بازدید نشود، یا می تواند شامل دور باشد.

3. اتصال و قطعیت

• اتصال: یک گراف گفته می شود که اتصال دارد اگر بین هر دو راس آن حداقل یک مسیر وجود داشته باشد.
• قطعیت: اگر با حذف یک راس یا یال، گراف به دو یا چند قسمت غیر متصل تقسیم شود، آن راس یا یال قطع کننده نامیده می شود.

کاربرد الگوریتم دایکسترا در سیستم های GPS

فرض کنید شما بخواهید از نقطه A به نقطه B در یک شهر بروید و می خواهید سریع ترین مسیر را برای رانندگی پیدا کنید. شبکه راه های شهر را می توان به صورت یک گراف وزن دار تصور کرد که در آن هر تقاطع یک راس و هر خیابان یک یال است، و وزن هر یال نشان دهنده زمان لازم برای عبور از آن خیابان است.

فرمول بندی:

گراف G=(V,E) را در نظر بگیرید، که در آن Vمجموعه رئوس (تقاطع ها) و E مجموعه یال ها (خیابان ها) است. به هر یال وزنی w(u,v) اختصاص داده می شود که می تواند زمان یا فاصله را نشان دهد.

الگوریتم دایکسترا با انتخاب راس مبدا s شروع می کند و فاصله های اولیه را به صورت زیر تنظیم می کند:

• d[s]=0 (فاصله راس مبدا از خودش صفر است)
  d[v]=∞ برای هر v≠s فاصله اولیه بین راس مبدا و سایر رئوس بینهایت در نظر گرفته می شود

سپس، الگوریتم به صورت تکراری کمترین فاصله موجود بین راس مبدا و یک راس u که هنوز بازدید نشده است را انتخاب می کند، و فاصله های مجاور آن را به روزرسانی می کند:
برای هر یال E(u,v)∈E که به u متصل است فرمول زیر برقرار است

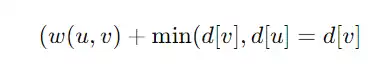
این فرایند تا زمانی ادامه پیدا می کند که همه رئوس بازدید شوند. در نهایت، d[v] کوتاه ترین فاصله از راس مبدا s به هر راس v را نشان می دهد.این داده ها مستقیما در سیستم های ناوبری مورد استفاده قرار می گیرند تا بهترین مسیر بر اساس شرایط جاری ترافیکی ارائه شود.

کاربرد هوش مصنوعی (AI) در نظریه گراف به ویژه در زمینه های تجزیه و تحلیل داده ها و بهینه سازی شبکه های پیچیده نقش بسیار مهمی دارد. هوش مصنوعی می تواند برای فهم بهتر و استخراج دانش از داده های ساختاریافته مانند شبکه ها و گراف ها استفاده شود. در ادامه، به چند نمونه از این کاربردها اشاره می کنیم:

1. بهینه سازی مسیر

هوش مصنوعی می تواند برای بهبود الگوریتم های مسیریابی مانند الگوریتم دایکسترا یا A* استفاده شود. AI می تواند پیش بینی های دقیق تری از زمان سفر و شرایط ترافیکی ارائه دهد با استفاده از داده های جمع آوری شده به صورت زنده و تحلیل های پیشرفته. این امر منجر به انتخاب بهترین مسیر ممکن در زمان واقعی می شود.

2. تحلیل شبکه های اجتماعی

هوش مصنوعی در تحلیل شبکه های اجتماعی برای شناسایی الگوهای تعاملات کاربران، کشف جوامع یا گروه هایی با علایق مشابه، و پیش بینی روابط بین کاربران استفاده می شود. مدل های یادگیری ماشینی می توانند به کشف خوشه ها و جوامع در گراف های بزرگ کمک کنند، که این امر می تواند در توسعه استراتژی های بازاریابی و سایر تحلیل های تجاری کاربرد داشته باشد.

3. سیستم های توصیه گر

هوش مصنوعی و نظریه گراف به طور مشترک در سیستم های توصیه گر برای پیشنهاد محصولات، خدمات یا محتوا به کاربران بر اساس ترجیحات و رفتارهای قبلی آن ها استفاده می شود. این سیستم ها اغلب با استفاده از گراف های کاربر-محصول ساخته می شوند که در آن یال ها نشان دهنده تعاملات یا روابط بین کاربران و محصولات هستند.

4. پردازش زبان طبیعی (NLP)

در زمینه NLP، گراف های معنایی برای نمایش روابط معنایی بین کلمات یا عبارات در یک جمله یا متن بزرگ تر استفاده می شوند. هوش مصنوعی می تواند به تحلیل و فهم بهتر ساختار و معنای متون کمک کند، مانند تشخیص نام ها، موجودیت ها، و روابط بین آن ها.

5. بیوانفورماتیک

در بیوانفورماتیک، گراف ها برای مدل سازی ساختارهای بیولوژیکی مانند شبکه های متابولیکی یا تعاملات پروتئینی استفاده می شوند. هوش مصنوعی می تواند در تحلیل این شبکه ها برای کشف مسیرهای بیولوژیکی جدید یا درک بهتر مکانیسم های بیماری ها کمک کنند.

یکی از مثال های برجسته ی استفاده از هوش مصنوعی و نظریه گراف در دنیای واقعی، سیستم های توصیه گر (Recommender Systems) است که در پلتفرم های بزرگ تجارت الکترونیک مانند آمازون به کار گرفته می شوند که این عملگر در ایران نسبت به پلتفرم های تجارت الکترونیک مانند سایت دیجی کالا و سایت باسلام ارائه می شود.

سیستم توصیه گر آمازون

آمازون از الگوریتم های پیچیده ی توصیه گر استفاده می کند تا محصولاتی را به کاربران پیشنهاد دهد که بر اساس تاریخچه ی خرید و جستجوی آن ها، ممکن است به آن علاقه مند باشند. این سیستم ها از گراف های کاربر-محصول استفاده می کنند که در آن رئوس نمایانگر کاربران و محصولات هستند و یال ها نشان دهنده ی تعاملات بین کاربران و محصولات می باشند، مانند خریدها، بررسی ها و امتیازدهی ها.

کاربرد هوش مصنوعی و نظریه گراف:

1. کشف پتانسیل مشتری: با تحلیل پیچیده ی گراف های کاربر-محصول، آمازون می تواند الگوهای خرید را شناسایی کند و محصولات مرتبط یا مکمل را به کاربران پیشنهاد دهد.
2. بهینه سازی سبد خرید: با استفاده از تحلیل گراف، آمازون می تواند محصولاتی را پیشنهاد دهد که به طور معمول با هم خریداری می شوند، این امر باعث افزایش میزان فروش و رضایت مشتری می شود.
3. پردازش طبیعی زبان و تحلیل احساسات: با استفاده از تکنیک های NLP بر روی نظرات و بررسی های کاربران، آمازون می تواند احساسات کاربران را نسبت به محصولات تجزیه و تحلیل کرده و این داده ها را برای بهبود پیشنهادات استفاده کند.
4. این سیستم ها با ترکیب هوش مصنوعی و نظریه گراف نه تنها به بهبود تجربه ی کاربر کمک می کنند بلکه باعث بهبود کارایی تجاری و فروش نیز می شوند. این نوع سیستم ها می توانند درک دقیق تری از نیازها و رفتارهای کاربران ارائه دهند و توانایی انطباق با تغییرات رفتاری کاربران در زمان واقعی را دارند.

نتیجه گیری

استفاده از هوش مصنوعی و نظریه گراف در کنار هم نه تنها امکان تجزیه و تحلیل دقیق تر و بهینه سازی فرایندهای مختلف را فراهم می کند، بلکه دروازه ای به سوی کشف دانش های جدید و پیشبرد فناوری ها می گشاید. این ترکیب قدرتمند به ما امکان می دهد که از داده های بزرگ، ساختاریافته و پیچیده، اطلاعات مفید و کاربردی استخراج کنیم.

در مثال سیستم توصیه گر آمازون، مشاهده کردیم که چگونه الگوریتم های مبتنی بر نظریه گراف و تکنیک های هوش مصنوعی می توانند به شناسایی الگوهای خرید کاربران و پیشنهاد محصولات بهینه کمک کنند. این توانایی نه تنها منجر به افزایش رضایت مشتری می شود، بلکه به عنوان ابزاری برای افزایش فروش و بهبود استراتژی های بازاریابی شرکت ها نیز عمل می کند.

به طور خلاصه، تلفیق هوش مصنوعی و نظریه گراف در برخورد با مسائل مختلف، از بهینه سازی مسیر در سیستم های ناوبری گرفته تا تحلیل شبکه های اجتماعی و بیوانفورماتیک، ابزاری قدرتمند را برای پیشبرد دانش و فناوری به دست ما می دهد. آینده ی تحقیقات در این حوزه ها قطعا شاهد استفاده گسترده تر و پیشرفت های بیشتر در این زمینه ها خواهد بود. این ترکیب، در عصر داده ها، بیش از پیش به یک ضرورت تبدیل شده است، زیرا افزایش حجم داده ها و پیچیدگی سیستم های مدرن تحلیل های سنتی را به چالش می کشد و نیاز به رویکردهای نوآورانه تر را طلب می نماید.