روش های شبه نیوتنی برای حل مسائل بهینه سازی غیرخطی

روش های شبه نیوتنی برای حل مسائل بهینه سازی غیرخطی (Quasi-Newton Methods)

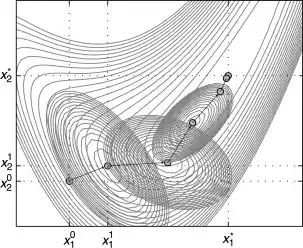
روش های شبه نیوتنی تکنیک های تکراری هستند که برای حل مسائل بهینه سازی غیرخطی استفاده می شوند. این روش ها زمانیکه محاسبه ماتریس هسین (مشتقات مرتبه دوم) بسیار هزینه بر یا مشکل است، استفاده می شوند.

این روش ها به گونه ای طراحی شده اند که نسبت به تکنیک های ساده تر مانند گرادیان کاهشی (نزولی)، کارآمدتر و قوی تر باشند، در حالیکه از پیچیدگی محاسباتی روش نیوتن، که نیاز به محاسبه و معکوس ماتریس هسین در هر تکرار دارد، اجتناب می کنند. به بیان دیگر، روش شبه نیوتنی از تقریب ماتریس هسین معکوس استفاده می نماید تا از هزینه محاسباتی و الزامات ذخیره سازی مرتبط با روش نیوتن جلوگیری کند. هدف این روش دستیابی به همگرایی فوق خطی( superlinear convergence) با استفاده از اطلاعات گرادیان و حافظه محدود است.

روش نیوتن از گرادیان (مشتق مرتبه اول) و ماتریس هسین (مشتقات مرتبه دوم) برای بدست آوردن نقطه بهینه یک تابع استفاده می کند. روش نیوتن از ماتریس هسین برای تعیین انحنای تابع استفاده می کند که به بدست آوردن مسیر جستجو و اندازه گام بهینه کمک می کند. با این حال، محاسبه و معکوس کردن ماتریس هسین می تواند از نظر محاسباتی گران باشد(به خصوص برای مسائل با ابعاد بالا).

روش های شبه نیوتنی با استفاده از اطلاعات گرادیان تکرارهای قبلی، ماتریس هسین را تقریب می زنند. این تقریب به طور مکرر به روز می شود و روش را کارآمدتر می کند.

اساس روش های شبه نیوتن در قوانین به روز رسانی یا آپدیت (update ) برای تقریب هسین است. این قوانین تضمین می کنند که تقریب ماتریس هسین مثبت معین باقی می ماند، که برای همگرایی الگوریتم بسیار مهم است.

الگوریتم تکراری شبه نیوتنی:

1- در هر تکرار، الگوریتم جهت جستجو را با استفاده از تقریب هسین و گرادیان تابع محاسبه می کند.

2- سپس یک جستجوی خطی برای تعیین اندازه بهینه طول گام در جهت جستجو انجام می شود.

3-نقطه جدید برای به آپدیت تقریب هسین استفاده می شود و این روند تا زمان همگرایی تکرار می شود.

مزایای روش های شبه نیوتنی

• عملکرد: روش های شبه نیوتنی عموما کارآمدتر از روش نیوتن هستند، زیرا از محاسبه و معکوس پرهزینه ماتریس هسین جلوگیری می کنند.
• مقاوم بودن(Robustness): این روش ها مقاوم هستند و می توانند طیف وسیعی از مسائل بهینه سازی غیرخطی را حل کنند.
• همگرایی: تحت شرایط خاص، روش های شبه نیوتنی می توانند به صورت فوق خطی همگرا شوند، به این معنی که خطا سریعتر از خطی کاهش می یابد.

روش های شبه نیوتنی متداول

• DFP (Davidon-Fletcher-Powell) Method
• BFGS ( Broyden-Fletcher-Goldfarb-Shanno) Method