کاربرد دیکانولوشن در سوزنسوزن پلاستیکی
به نام خدا

برای بررسی علمی کاربرد روشهای دیکانولوشن (Deconvolution) در تحلیل ارتفاع پالس خام حاصل از یک سوزنسوزن پلاستیکی (Plastic Scintillator)، ابتدا باید مفاهیم پایه، چالشها، و روشهای مرتبط را درک کنیم. در ادامه، مروری ساختاریافته بر این موضوع ارائه میشود:
۱. مقدمه و مفاهیم کلیدی
۱.۱. سوزنسوزن پلاستیکی (Plastic Scintillator)
- سوزنسوزنهای پلاستیکی مواد شفافی هستند که در اثر برهمکنش با ذرات پرانرژی (مانند ذرات آلفا، بتا، نوترونها، یا پرتوهای گاما) نور مرئی منتشر میکنند.
- ارتفاع پالس خام (Raw Pulse Height) متناسب با انرژی ذره ورودی است و برای تعیین طیف انرژی استفاده میشود.
- مشکل اصلی: سیگنالهای اندازهگیریشده اغلب به دلیل پاسخ غیرایدهآل سیستم (نویز الکترونیکی، تاخیر زمانی، اتلاف انرژی، و ...) تحریف میشوند.
۱.۲. کانولوشن (Convolution) و دیکانولوشن (Deconvolution)
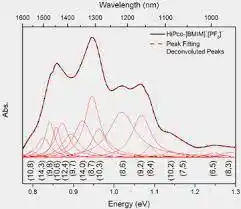
- کانولوشن: فرآیندی که در آن سیگنال اصلی (x(t)) با تابع پاسخ سیستم (h(t)) ترکیب میشود و سیگنال تحریفسازیشده (y(t)=x(t)∗h(t)+نویز) را تولید میکند.
- دیکانولوشن: فرآیند معکوس برای بازیابی سیگنال اصلی (x(t)) از سیگنال اندازهگیریشده (y(t)) با حذف اثرات سیستم (h(t)).
۲. دلایل نیاز به دیکانولوشن در سوزنسوزنها
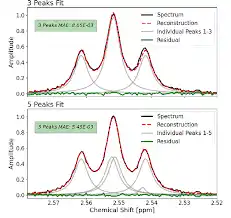
۱. بهبود تفکیکپذیری انرژی: پاسخ سیستم ممکن است باعث پهنشدن پیکها در طیف انرژی شود.
۲. حذف نویز و آرتیفکتها: اثرات نویز الکترونیکی یا تداخلات خارجی.
۳. بازیابی سیگنالهای با فرکانس بالا: بازیابی جزئیات از دسترفته در فرآیند اندازهگیری.
۳. روشهای دیکانولوشن
۳.۱. روشهای کلاسیک
- دیکانولوشن وینر (Wiener Deconvolution):
ترکیب فیلتر معکوس با تنظیم نویز.
مناسب برای سیستمهای با پاسخ خطی و نویز گاوسی. - روش ریچاردسون-لوسی (Richardson-Lucy):
مبتنی بر بیشینهسازی احتمال (Maximum Likelihood) برای سیستمهای پویسان.
مناسب برای دادههای با نویز پواسون (مثلا در شمارش ذرات). - فیلتر تطبیقی (Adaptive Filtering):
برای سیستمهای با پاسخ متغیر با زمان.
۳.۲. روشهای پیشرفته
- دیکانولوشن غیرکور (Non-Blind):
اگر تابع پاسخ سیستم (h(t)) از قبل شناختهشده باشد.
مثال: استفاده از تابع پاسخ ضربه (Impulse Response) سیستم. - دیکانولوشن کور (Blind Deconvolution):
هنگامی که h(t) ناشناخته است و باید همزمان با سیگنال اصلی تخمین زده شود.
نیازمند الگوریتمهای پیچیده مانند روشهای مبتنی بر یادگیری عمیق.
۴. مراحل پیادهسازی دیکانولوشن
۱. اندازهگیری تابع پاسخ سیستم:
- استفاده از منابع کالیبرهشده (مثلا ذرات با انرژی مشخص) برای استخراج h(t).
۲. پیشپردازش دادهها: - حذف نویز پایه (Baseline Noise) با فیلترهای پایینگذر.
- نرمالسازی سیگنالها.
۳. اجرای الگوریتم دیکانولوشن: - انتخاب روش متناسب با نوع نویز و سیستم.
۴. اعتبارسنجی نتایج: - مقایسه با دادههای شبیهسازیشده یا آزمایشهای کنترلشده.
۵. چالشها و محدودیتها
- حساسیت به نویز: دیکانولوشن میتواند نویز را تقویت کند (مشکل Ill-Posed).
- نیاز به محاسبات سنگین: روشهایی مانند ریچاردسون-لوسی نیازمند تکرارهای زیاد.
- وابستگی به دقت تابع پاسخ: خطا در تخمین h(t) منجر به انحراف نتایج میشود.
۶. مثالهای کاربردی
- طیفسنجی گاما: بهبود تفکیک پیکهای انرژی در آشکارسازهای سوزنسوزنی.
- تصویربرداری پزشکی: بازسازی تصاویر در PET (Positron Emission Tomography) با استفاده از سوزنسوزنها.
- پایش تشعشعات: افزایش دقت در اندازهگیری شار ذرات پرانرژی.
۷. ابزارها و نرمافزارهای پیشنهادی
- پایتون: کتابخانههای
SciPy(توابعwienerوdeconvolve) وTensorFlowبرای روشهای مبتنی بر یادگیری عمیق. - MATLAB: جعبهابزار Signal Processing.
- ROOT Framework: برای تحلیل دادههای فیزیک هستهای.
۸. منابع علمی پیشنهادی
- کتابها:
Signal Recovery from Noise in Electronic Instrumentation by T. H. Wilmshurst.
Deconvolution of Images and Spectra توسط پی. ای. جانسون. - مقالات:
"Application of Richardson-Lucy Algorithm in Scintillator Signal Processing" (Journal of Instrumentation).
"Blind Deconvolution for Gamma-Ray Spectroscopy" (IEEE Transactions on Nuclear Science).
۹. نتیجهگیری
استفاده از دیکانولوشن در پردازش سیگنالهای سوزنسوزن پلاستیکی میتواند تفکیکپذیری انرژی و دقت اندازهگیری را بهبود بخشد. انتخاب روش مناسب (مانند وینر یا ریچاردسون-لوسی) به نوع نویز، دانش پیشینی از سیستم، و منابع محاسباتی بستگی دارد. برای شروع، پیشنهاد میشود ابتدا با دادههای شبیهسازیشده و توابع پاسخ شناختهشده آزمایشها را انجام دهید تا از اعتبار روش اطمینان حاصل کنید.
پایان
دانشگاه تحصیلات تکمیلی صنعتی و فناوری پیشرفته شاهین جلیل پور