تکنیک های کاهش ابعاد برای داده ها با ابعاد بالا

تحلیل مولفه های اصلی (PCA): یک تکنیک پرکاربرد برای کاهش ابعاد داده ها از طریق یافتن ترکیبات خطی متعامد به نام مولفه های اصلی است. این روش خطی و بدون نظارت در زمینه های مختلف علمی و مهندسی به کار می رود و در مقایسه با روش GLCM دقت بالایی در تشخیص تصویر دارد. با این حال، PCA محدود به زیر فضاهای خطی است و مشخص نیست که چه تعداد مولفه اصلی باید نگه داشته شود. همچنین، Sparse PCA به عنوان یک روش جدید در این حوزه به تازگی مورد توجه قرار گرفته است.

PCA توزیع شده (DPCA) با تقسیم داده ها به صورت افقی یا عمودی، بار محاسباتی تکنیک PCA را کاهش می دهد. در تقسیم بندی افقی، داده ها به نمونه های n و در تقسیم بندی عمودی به متغیرهای d تقسیم می شوند. این روش زمانی مفید است که اندازه نمونه بزرگ باشد یا داده ها در مکان های مختلف قرار داشته باشند. نرخ خطای DPCA مشابه PCA سنتی است، اما پیچیدگی محاسباتی آن حداقل O(d³) است که می تواند در داده های بزرگ دشوار باشد.

همچنین، الگوریتم FADI که توسط Shuting و همکاران پیشنهاد شده، به توسعه PCA با توزیع سریع کمک می کند.

پیچیدگی PCA سنتی برابر است باO(d²n + d³) ، پیچیدگی سریع PCA برابر است باO(dnK + d²K) ، پیچیدگی PCA توزیع شده برابر است با O(d²√nr + d³). همچنین، پیچیدگی FADI برابر است با O(nK² + d²K² log n) می باشد.

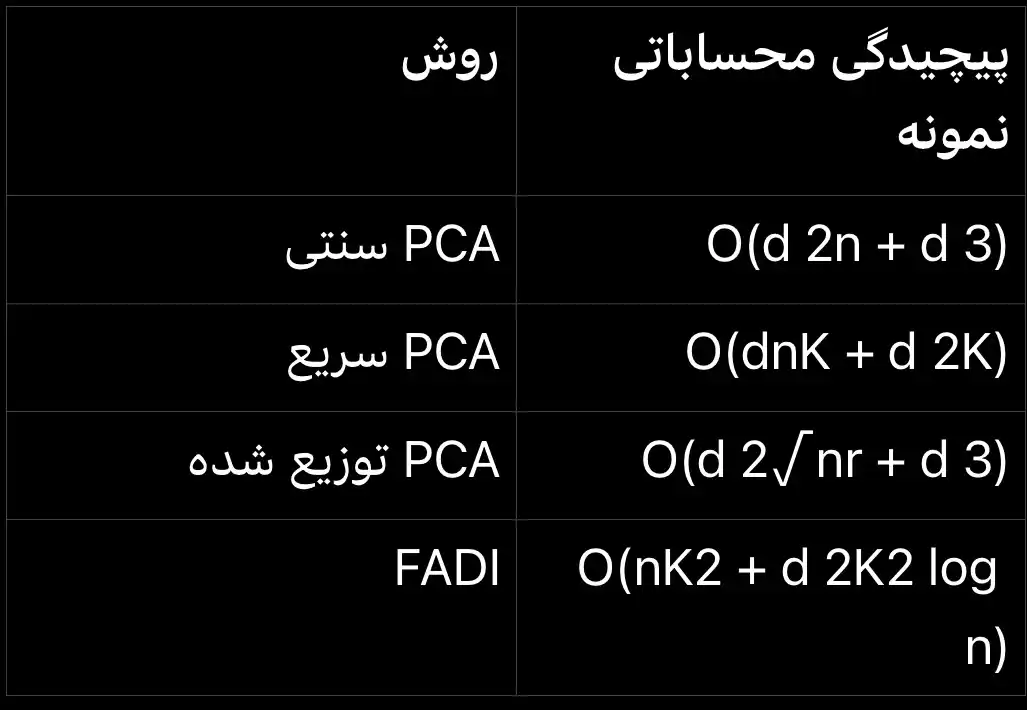
پیچیدگی PCA سنتی برابر است باO(d²n + d³) ، پیچیدگی سریع PCA برابر است باO(dnK + d²K) ، پیچیدگی PCA توزیع شده برابر است با O(d²√nr + d³). همچنین، پیچیدگی FADI برابر است با O(nK² + d²K² log n) می باشد.

تحلیل عاملی (FA):یک روش خطی بدون نظارت است که ویژگی های جدیدی از ویژگی های مشاهده شده ایجاد می کند تا ویژگی های مشترک را نمایندگی کند. مدل آن وابسته به تعداد متغیرها نیست و متغیرها به عوامل مشترک ناشناخته وابسته اند. FA مزایای خاصی دارد، مانند توانایی استفاده از ویژگی های ذهنی و عینی و شناسایی ابعاد پنهان، اما معایبی نیز دارد، از جمله خطر از دست دادن ویژگی های مهم و دشواری در نام گذاری عوامل.

تحلیل تشخیص خطی (LDA): یک روش نظارت شده برای کاهش ابعاد است که در کاربردهایی مانند تشخیص گفتار و چهره استفاده می شود.

الگوریتم MMC-SPP که توسط Ya LI پیشنهاد شده، برای تشخیص عنبیه استفاده می شود و بر اساس معیار حداکثر حاشیه (MMC) و تصویرسازی حفظ ساختار (SPP) عمل می کند. ابتدا، داده های ابعاد بالا به زیرسیستم هایی تقسیم شده و سپس با استفاده از SPP ابعاد ویژگی های عنبیه کاهش می یابد. MMC، به عنوان یک روش یادگیری نظارت شده بهبود یافته از LDA، مشکل حجم نمونه کوچک را حل کرده و کاهش محاسبات را فراهم می کند.

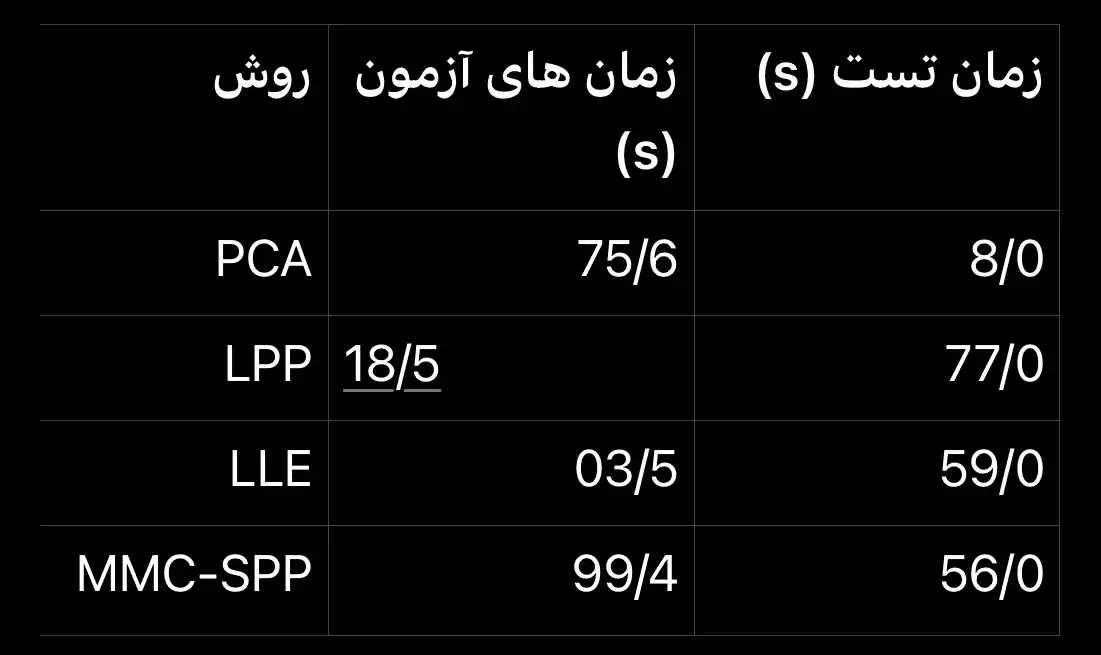
MMC-SPP با کوتاه ترین زمان اجرا و بالاترین بازدهی در تشخیص عنبیه به دلیل توانایی در یافتن ویژگی های بهینه و حذف ویژگی های زائد، برای تشخیص در زمان واقعی مناسب است.

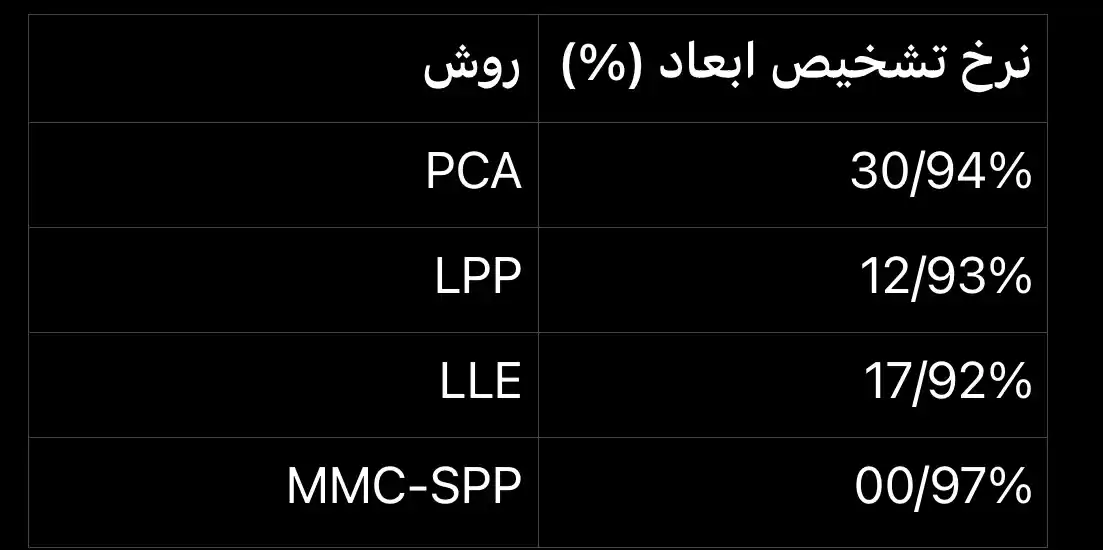
MMC-SPP بالاترین نرخ تشخیص را دارد که به 00/97% می رسد و از الگوریتم های PCA، LLE و LPP برتری دارد، همانطور که در جدول (۴) نیز نشان داده شده است.

تصویرسازی تصادفی (Random Projections)

روش تصویرسازی تصادفی یک تکنیک ساده و قدرتمند برای کاهش ابعاد است که از ماتریس های تصویرسازی برای تصویر کردن داده ها در فضاهای با ابعاد کمتر استفاده می کند.ستون های این ماتریس ها نمونه هایی از متغیرهای مستقل و هم توزیع (i.i.d.) با میانگین صفر و توزیع نرمال هستند. این روش عموما در زمینه خوشه بندی اسناد متنی با ابعاد بزرگ استفاده می شود. ابعاد اولیه در حدود ۶۰۰۰ و ابعاد نهایی نیز در حدود ۱۰۰ است. تصویرسازی تصادفی در مرحله پیش پردازش داده ها استفاده می شود.

مقیاس بندی چندبعدی وزنی (WMDS) نیز الگوریتمی است که داده های با ابعاد بالا را به فرم دو بعدی تبدیل می کند و به تحلیلگران امکان می دهد اطلاعات پیچیده را به راحتی بررسی کنند. WMDS با پیشگیری از محدودیت های بصری تکنیک های تجسم ابعادی بالا، دسترسی به داده های متعدد را تسهیل می کند.

تقریب منیفولد یکنواخت و طرح ریزی (UMAP)

UMAP یک الگوریتم بسیار موثر برای هر دو تجسم و کاهش ابعاد است. استفاده از الگوریتم UMAP سریع تر از t-SNE است و مقیاس پذیری بهتری ارائه می دهد. این روش تعبیه های با کیفیت بالا برای مجموعه داده های بزرگ تری نسبت به روش های قبلی تولید می کند. الگوریتم UMAP به دلیل کاربرد و اثربخشی اش در زمینه های مختلف علمی استفاده می شود. توصیف نظری الگوریتم بر اساس مجموعه های فازی ساده شده است. این روش می تواند به صورت یک گراف وزن دار توصیف شود. به این معنا که از نظر عملی، UMAP را می توان در قالب ساخت و عملیات روی گراف های وزن دار توصیف کرد. به ویژه این موضوع UMAP را در دسته الگوریتم های یادگیری گراف مبتنی بر همسایه k (مانند نقشه های خاص لاپلاسی، ایزومپ و t-SNE) قرار می دهد. از آنجایی که UMAP بر اساس فاصله بین مشاهدات و نه ویژگی های منبع است، نمی تواند معادلی از بارگذاری عاملی که تکنیک های خطی مانند PCA یا تحلیل عاملی ارائه می دهند، داشته باشد. برای تفسیرپذیری بحرانی، تکنیک های خطی مانند PCA، NMF یا PLS مناسب هستند .

نتیجه گیری

فرآیند کاهش ابعاد بسیار پیچیده است، بنابراین هیچ روش واحدی برای تمام موقعیت ها مناسب نیست. برای بهبود کارایی، استفاده از یک روش تنها کافی نیست و به همین دلیل از تکنیک های ترکیبی (هیبرید) کاهش ابعاد استفاده می شود.