ضرایب لاگرانژ و کاربرد آنها در یادگیری ماشین(SVM)

 مقدمه

در یادگیری ماشین و به ویژه در روش های بهینه سازی، اغلب با مسائلی مواجه می شویم که در آنها باید یک تابع هدف (Objective Function) را تحت یک یا چند محدودیت (Constraint) بهینه سازی کنیم. یکی از روش های قدرتمند برای حل اینگونه مسائل، استفاده از ضرایب لاگرانژ (Lagrange Multipliers) است. این روش به ما کمک می کند تا مسائل بهینه سازی با محدودیت ها را به مسائل بدون محدودیت تبدیل کنیم و سپس به راحتی آنها را حل کنیم.

در این مقاله، به طور کامل به بررسی ضرایب لاگرانژ می پردازیم و نشان می دهیم که چگونه می توان از این روش در یادگیری ماشین استفاده کرد. در نهایت، این مقاله به عنوان پیش نیازی برای درک روش ماشین بردار پشتیبان (Support Vector Machine - SVM) خواهد بود که در آن از ضرایب لاگرانژ برای بهینه سازی استفاده می شود.

_{1. مسئله بهینه سازی با محدودیت}

فرض کنید می خواهیم یک تابع هدف f(x) را بهینه سازی کنیم، اما این بهینه سازی باید تحت یک محدودیت g(x)=0 انجام شود. به عبارت دیگر، می خواهیم مقدار f(x) را کمینه یا بیشینه کنیم، به شرطی که g(x)=0 برقرار باشد.

به عنوان مثال، در یادگیری ماشین، ممکن است بخواهیم یک تابع خطا (Loss Function) را کمینه کنیم، اما در عین حال، پارامترهای مدل باید یک سری محدودیت ها را رعایت کنند. اینجاست که ضرایب لاگرانژ به کمک ما می آیند.

_{2. ضرایب لاگرانژ}

ضرایب لاگرانژ روشی است که به ما اجازه می دهد مسائل بهینه سازی با محدودیت ها را به مسائل بدون محدودیت تبدیل کنیم. این کار با معرفی یک تابع جدید به نام تابع لاگرانژ (Lagrangian Function) انجام می شود.

_{2.1 تابع لاگرانژ}

تابع لاگرانژ L(x,λ) به صورت زیر تعریف می شود:

L(x,λ)=f(x)−λ⋅g(x)

در اینجا:

• f(x) تابع هدفی است که می خواهیم آن را بهینه سازی کنیم.
• g(x)=0 محدودیتی است که باید رعایت شود.
• λ ضریب لاگرانژ است که به عنوان یک متغیر جدید معرفی می شود.
• 
  

_{2.2 چرا تابع لاگرانژ؟}

تابع لاگرانژ به ما کمک می کند تا محدودیت g(x)=0 را درون تابع هدف ادغام کنیم. به عبارت دیگر، به جای اینکه مستقیم ا f(x) را تحت محدودیت g(x)=0 بهینه سازی کنیم، تابع لاگرانژ را بهینه سازی می کنیم که شامل هر دو تابع f(x) و g(x) است.

_{2.3 شرایط بهینه سازی}

برای یافتن نقاط بهینه، باید مشتقات جزئی تابع لاگرانژ را نسبت به x و λ محاسبه کرده و آنها را برابر صفر قرار دهیم:

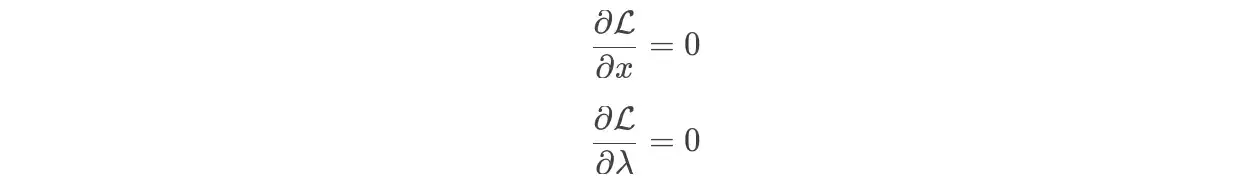
این معادلات به ما کمک می کنند تا مقادیر بهینه x و λ را پیدا کنیم.

_{3. کاربرد در یادگیری ماشین}

در یادگیری ماشین، ضرایب لاگرانژ اغلب در روش هایی مانند ماشین بردار پشتیبان (SVM) استفاده می شوند. در SVM، هدف این است که یک مرز تصمیم گیری (Decision Boundary) پیدا کنیم که حاشیه (Margin) بین دو کلاس را بیشینه کند. این مسئله یک مسئله بهینه سازی با محدودیت است که با استفاده از ضرایب لاگرانژ حل می شود.

در SVM، تابع هدف به صورت زیر است:

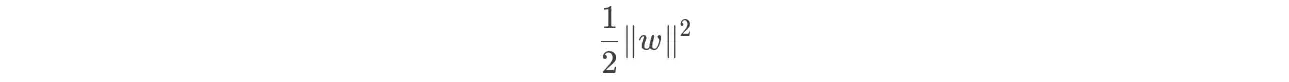
که باید تحت محدودیت های زیر کمینه شود:

تابع لاگرانژ برای این مسئله به صورت زیر تعریف می شود:

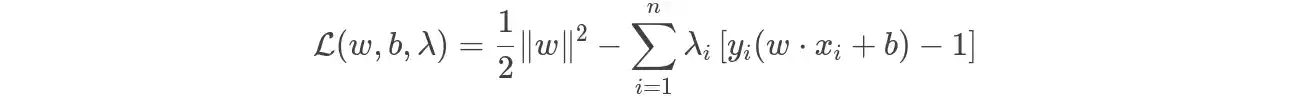
با حل این تابع لاگرانژ، می توانیم مقادیر بهینه w و b را پیدا کنیم که مرز تصمیم گیری بهینه را تعیین می کنند.

5. نتیجه گیری

ضرایب لاگرانژ یک ابزار قدرتمند در بهینه سازی مسائل با محدودیت ها هستند. با استفاده از این روش، می توانیم مسائل پیچیده ای را که در یادگیری ماشین با آنها مواجه می شویم، به مسائل ساده تر تبدیل کنیم و به راحتی آنها را حل کنیم. در مقاله بعدی، به طور مفصل به بررسی روش ماشین بردار پشتیبان (SVM) خواهیم پرداخت و نشان خواهیم داد که چگونه از ضرایب لاگرانژ در این روش استفاده می شود.