بهینه سازی غیرخطی مقیدNonlinear Constrained Optimization

روش های حل مسائل بهینه سازی غیرخطی

بهینه سازی غیرخطی مقید شامل کمینه سازی یا بیشینه سازی یک تابع هدف غیرخطی است که توابع قیدی آن نیز می توانند غیرخطی باشند. 

حل مسائل بهینه سازی غیرخطی مقید، به دلیل وجود تابع هدف و یا قیدهای غیرخطی، پیچیده تر از مسائل بهینه سازی نامقید است. روش های مختلفی برای حل این مسائل توسعه داده شده اند که اغلب از اطلاعات مشتقات مرتبه اول (مبتنی بر گرادیان) یا مرتبه دوم (مبتنی بر هسین) استفاده می کنند.

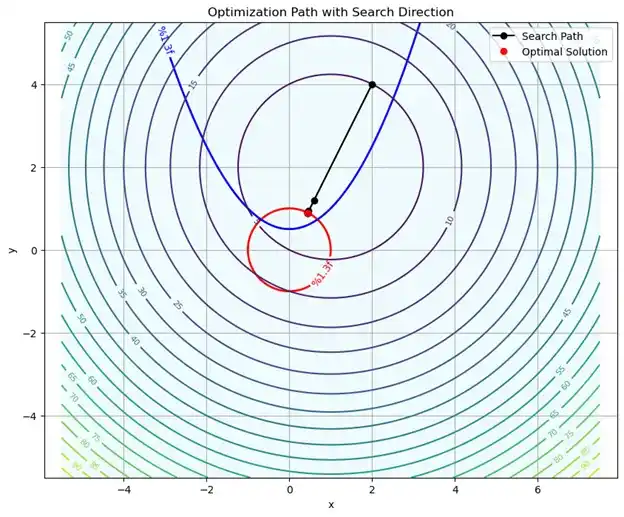
ضرایب لاگرانژ(Lagrange Multipliers): 

این روش شامل استفاده از ضرایب لاگرانژ برای تبدیل مسئله مقید به یک مسئله نامقید می باشد. این روش به ویژه برای مسائلی با قیدهای تساوی مفید است. در این روش قیدهای مساوی و تابع هدف بصورت یک تابع وزنی (ضرایب لاگرانژ بعنوان وزن ها) نوشته می شوند تا مساله بهینه سازی نامقید گردد و سپس حل می شود.

شرایط کاروش-کوهن-تاکر (KKT): 

برای مسائلی با قیدهای مساوی و نامساوی، شرایط KKT شرایط لازم مرتبه اول برای بهینگی را فراهم می کنند. این شرایط به شناسایی جواب های شدنی که در قیدها صدق می کنند، کمک می کند.

برنامه ریزی درجه دوم متوالی (SQP):

اساس این روش تقریب مسئله بهینه سازی غیرخطی با دنباله ای از زیرمسئله های درجه دوم می باشد. به بیان دیگر، در هر تکرار، مسئله غیرخطی اصلی را با یک تابع هدف درجه دوم و قیدهای خطی شده تقریب می زند.

در اصل، روش SQP یک مسئله بهینه سازی غیرخطی پیچیده را به مجموعه ای از زیرمسئله های درجه دوم ساده تر تجزیه می کند که حل عددی آنها آسان تر است. این فرآیند تکراری به همگرایی به سمت جواب بهینه کمک می کند.

روش تابع جریمه(Penalty function methods):

 این روش ها با افزودن یک عبارت جریمه برای نقض قیدها، قیدهای مساله را در تابع هدف لحاظ می کنند. سپس روش حل مساله بهینه سازی روی این تابع هدف اصلاح شده اجرا می شود.

روش تابع مانع(Barrier function methods):

 مشابه روش های تابع جریمه، روش تابع مانع یک عبارت مانع به تابع هدف اضافه می کنند که با نزدیک شدن جواب به مرز ناحیه شدنی(feasible region)، به بی نهایت میل می کند. این کار باعث می شود جواب در طول حل مساله بهینه سازی در ناحیه شدنی باقی بماند.

ادامه دارد....