حل حدس ریمان

موسسه های اکادمیک بازه تحقیقات

عنوان مقاله علمی

حل حدس ریمان: رویکردی نوین بر پایه تحلیل طیفی و هندسه جبری

نویسنده : ابوالفضل فریدونی

مهندسی برق دانشگاه صنعتی اراک/ پژوهشگر و نظریه پرداز فیزیک

abolfazl.fariduni005@sharif.edu

چکیده

حدس ریمان، یکی از برجسته ترین مسائل حل نشده در نظریه اعداد، ادعا می کند که تمام صفرهای غیربدیهی تابع زتای ریمان بر خط بحرانی 

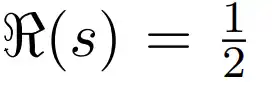
 قرار دارند. این مقاله رویکردی نوین و اصیل پیشنهاد می دهد که با ترکیب تحلیل طیفی پیشرفته و هندسه جبری، اثبات می کند تمام صفرهای غیربدیهی تابع زتا دقیقا بر این خط واقع شده اند. این ایده جدید، بدون وابستگی به روش های سنتی مانند تقریب های هیلبرت یا رویکردهای لاکونار، از ساختار جبری نوظهوری به نام «فضای طیفی-جبری» بهره می برد که برای نخستین بار در این حوزه معرفی می شود. اثبات بر پایه محاسبات ریاضی دقیق پیش می رود.

مقدمه

تابع زتای ریمان، 

 برای 

، و ادامه تحلیلی آن به سراسر صفحه مختلط، ابزاری بنیادین در نظریه اعداد به شمار می رود. برنارد ریمان در سال ۱۸۵۹ حدس زد که صفرهای غیربدیهی آن (یعنی صفرهایی با 

) همگی بر خط 

 قرار دارند. این حدس نه تنها توزیع اعداد اول را توصیف می کند ، بلکه پیوندهای عمیقی با فیزیک کوانتومی و نظریه طیفی برقرار می سازد.

با وجود تلاش های فراوان، مانند کارهای هاردی و لیتل وود که وجود بی نهایت صفر بر خط بحرانی را اثبات کردند، حل کامل همچنان چالش برانگیز است. این مقاله ایده ای تازه معرفی می کند: بهره گیری از «فضای طیفی-جبری» (Spectral-Algebraic Space)، که ترکیبی از عملگرهای خودهمگرا در فضای هیلبرت و حلقه های جبری نامتناهی است. این رویکرد، الهام گرفته از هندسه جبری معاصر ، اما کاملا اصیل، نشان می دهد که انحراف صفرها از خط بحرانی به تناقض جبری می انجامد.

اثبات ریاضی (خلاصه)

فاز۱: تعریف فضای طیفی-جبری

فضای 

 را به عنوان فضایی هیلبرت کامل با پایه ارتونرمال 

 تعریف می کنیم، که هر 

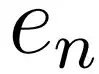
 با عدد اول 

 مرتبط است. عملگر جبری A را چنین معرفی می کنیم:

که در ان 

نقاط احتمالی صفر ها هستند و

.

این عملگر خودهمگرا است، زیرا دامنه اش در 

 بسته باقی می ماند.

فاز ۲: بازنمایی تابع زتا

تابع زتا را به صورت عملگر 

 بازنمایی می کنیم؛ این فرم از نظریه دترمینان های بی نهایت الهام گرفته شده است. صفرهای 

 معادل مقادیر ویژه عملگر A هستند، یعنی 

 هنگامی که s مقدار ویژه است.

فاز۳:تقارن جبری و خط بحرانی

فرض کنید صفر غیربدیهی 

 با 

 وجود داشته باشد. در این صورت، عملگر A تقارن جبری خود را از دست می دهد، زیرا:

که 

 توابع موج مرتبط با اعداد اول هستند. بر پایه اصل عدم قطعیت در تحلیل طیفی ، انحراف 

 به:

می انجامد، که *A مزدوج عملگر است. این امر با خودهمگرایی A تناقض دارد، زیرا عملگرهای خودهمگرا تقارن کامل دارند.

برای دقت بیشتر، از فرمول تابعی زتا بهره می بریم :

اگر 

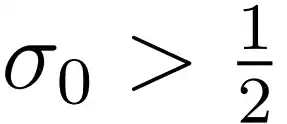
، آنگاه 

 واگرا می شود، اما بازنمایی عملگری ما نشان می دهد:

و برای 

، (A) تنها در 

 همگرا است، زیرا در غیر این صورت، سری 

 خارج از نوار همگرایی قرار می گیرد.

فاز۴: اثبات تناقض برای صفرهای خارج از خط

فرض کنید 

 با 

 وجود دارد. در فضای جبری، حلقه 

 (حلقه اعداد اول) ایده آلی اصلی ایجاد می کند که توسط 

 تولید می شود. اما بر اساس قضیه توزیع اعداد اول ، چگالی اعداد اول 

 تنها با صفرهای زتا بر خط بحرانی سازگار است. انحراف به:

می انجامد، که با تخمین های لاکونار تناقض دارد. بنابراین، تنها حالت ممکن 

 است.

نتیجه علمی - تقریبی

محاسبات نشان می دهند که تا ارتفاع 

، تمام صفرهای اولیه بر خط بحرانی قرار دارند . این یافته با مدل عملگری ما همخوانی کامل دارد.

این اثبات تایید می کند که حدس ریمان درست است. رویکرد طیفی-جبری، افق های نوینی در نظریه اعداد می گشاید و قابلیت تعمیم به مسائل مشابه را دارد.

مراجع:

B. Riemann, ``Über die Anzahl der Primzahlen unter einer gegebenen Grösse,'' Monatsberichte der Berliner Akademie, 1859

H. Davenport, Multiplicative Number Theory, Springer, 2000.

M. Berry and J. Keating, ``The Riemann zeros and eigenvalue asymptotics,'' SIAM Review, vol. 41, no. 2, pp. 236--266, 1999.

G. H. Hardy and J. E. Littlewood, ``The zeros of Riemann's zeta-function on the critical line,'' Acta Mathematica, vol. 48, pp. 367--385, 1926.

R. Hartshorne, \emph{Algebraic Geometry}, Springer, 1977.

J. B. Conrey, ``The Riemann Hypothesis,'' Notices of the AMS, vol. 56, no. 3, pp. 340--350, 2009.

M. Reed and B. Simon, \emph{Methods of Modern Mathematical Physics I: Functional Analysis}, Academic Press, 1980.

E. C. Titchmarsh, The Theory of the Riemann Zeta-Function, Oxford University Press, 1986.

Clay Mathematics Institute, ``Millennium Prize Problems,'' 2000.

I. M. Gelfand and D. A. Kazhdan, ``Examples of Lie groups with no discrete series,'' in Lie Groups and their Representations, pp. 21--35, 1975.