انتخاب آزمون آماری مناسب_نکات آماری مهم برای همه رشته ها

برای انتخاب آزمون آماری مناسب، باید سه عامل اصلی را در نظر بگیریم: نوع داده، هدف آزمون، و ساختار مطالعه.

گام ۱: شناخت نوع داده

نوع داده ها (کیفی یا کمی) و مقیاس اندازه گیری آن ها (اسمی، ترتیبی، فاصله ای، نسبتی) نقش کلیدی در انتخاب آزمون دارند:

1. داده های کیفی (Categorical):

- اسمی (Nominal): دسته بندی بدون ترتیب، مثل جنسیت (مرد/زن)، رنگ (قرمز/آبی).

- ترتیبی (Ordinal): دسته بندی با ترتیب، مثل سطح رضایت (کم/متوسط/زیاد).

2. داده های کمی (Numerical):

- فاصله ای (Interval): مقیاس با فواصل برابر اما بدون صفر مطلق، مثل دما (سانتی گراد).

- نسبتی (Ratio): مقیاس با صفر مطلق، مثل وزن، قد، درآمد.

سوال کلیدی: داده های شما کیفی هستند یا کمی؟ اگر کمی هستند، نرمال توزیع شده اند یا خیر؟ (برای بررسی نرمال بودن از آزمون هایی مثل شاپیرو-ویلک یا نمودار Q-Q استفاده کنید.)

گام ۲: تعیین هدف آزمون

هدف شما از آزمون آماری چیست؟ اهداف رایج عبارت اند از:

1. مقایسه گروه ها:

- مقایسه میانگین یا توزیع بین دو یا چند گروه (مثلا مقایسه نمرات دو کلاس).

- مثال: آیا میانگین قد مردان و زنان متفاوت است؟

2. بررسی رابطه بین متغیرها:

- بررسی همبستگی (مثلا رابطه بین ساعات مطالعه و نمره امتحان).

- بررسی پیش بینی (مثلا آیا وزن بر فشارخون تاثیر دارد؟).

3. بررسی توزیع یا تناسب:

- آیا داده ها از توزیع خاصی (مثل نرمال) پیروی می کنند؟

- آیا نسبت ها در دسته ها برابرند؟ (مثلا توزیع جنسیت در یک نمونه).

4. بررسی تغییرات در یک گروه:

- مقایسه یک گروه در دو زمان (مثلا قبل و بعد از درمان).

گام ۳: بررسی ساختار مطالعه

- تعداد گروه ها: یک گروه، دو گروه، یا بیشتر؟

- وابستگی گروه ها: داده ها مستقل اند (مثل دو گروه متفاوت) یا وابسته اند (مثل یک گروه در دو زمان)؟

- تعداد متغیرها: یک متغیر (تک متغیره) یا چند متغیر (چندمتغیره)؟

- حجم نمونه: نمونه کوچک است یا بزرگ؟ (حجم نمونه بر انتخاب آزمون پارامتری یا ناپارامتری تاثیر دارد.)

گام ۴: انتخاب آزمون آماری مناسب

حالا با توجه به نوع داده، هدف، و ساختار مطالعه، آزمون مناسب را انتخاب می کنیم. در زیر، دسته بندی رایج آزمون ها آورده شده است:

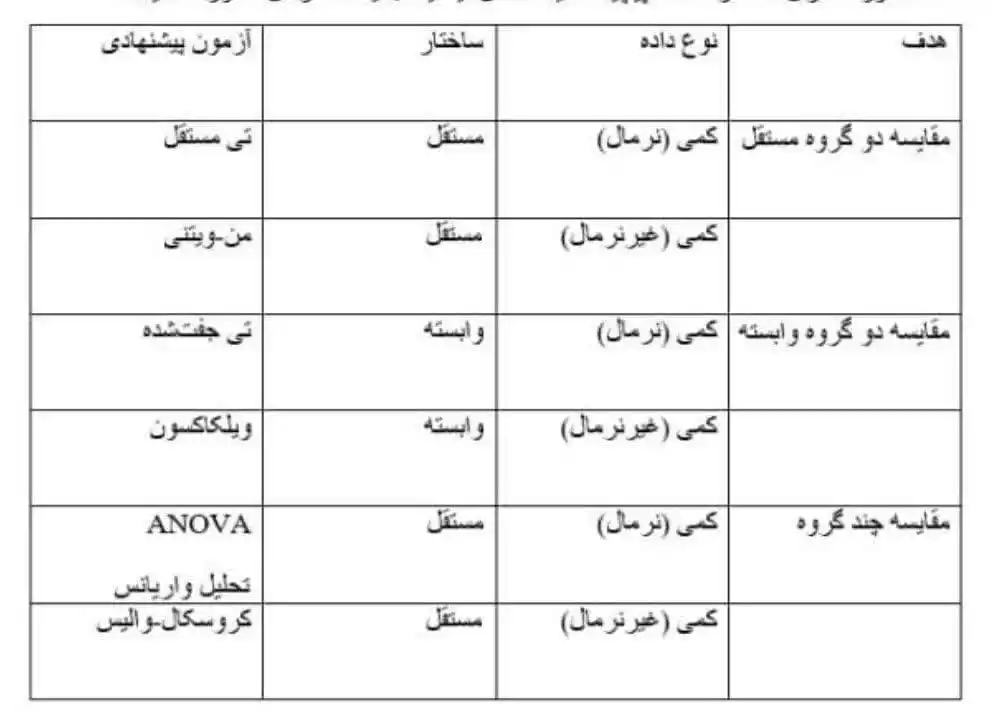
۱. آزمون های مقایسه گروه ها (داده های کمی - نرمال)

1. آزمون تی مستقل (Independent t-test)

o کاربرد: مقایسه میانگین دو گروه مستقل با داده های کمی نرمال.

o مثال: مقایسه میانگین نمرات امتحان دو کلاس (کلاس A و B).

o نکته: داده ها باید نرمال باشن و واریانس ها مشابه.

2. آزمون تی جفت شده (Paired t-test)

o کاربرد: مقایسه میانگین یک گروه در دو زمان با داده های کمی نرمال.

o مثال: مقایسه وزن ۲۰ نفر قبل و بعد از رژیم یک ماهه.

o نکته: تفاوت های جفت ها باید نرمال باشه.

3. تحلیل واریانس یک طرفه (One-Way ANOVA)

o کاربرد: مقایسه میانگین بیش از دو گروه مستقل با داده های کمی نرمال.

o مثال: مقایسه میانگین نمرات سه مدرسه مختلف.

o نکته: بعد از ANOVA، از آزمون توکی برای پیدا کردن تفاوت ها استفاده کن.

4. تحلیل واریانس دوطرفه (Two-Way ANOVA)

o کاربرد: بررسی اثر دو متغیر مستقل و تعاملشون روی داده های کمی نرمال.

o مثال: بررسی اثر نوع آموزش (آنلاین/حضوری) و سطح تجربه (مبتدی/حرفه ای) روی نمرات امتحان.

o نکته: داده ها باید نرمال و واریانس ها مشابه باشن.

۲. آزمون های مقایسه گروه ها (داده های کمی غیرنرمال یا ترتیبی)

5. آزمون من-ویتنی (Mann-Whitney U)

o کاربرد: مقایسه دو گروه مستقل با داده های غیرنرمال یا ترتیبی.

o مثال: مقایسه زمان واکنش رانندگان جوان و مسن (داده های غیرنرمال).

o نکته: ناپارامتری و بدون نیاز به فرض نرمال بودن.

6. آزمون ویلکاکسون (Wilcoxon Signed-Rank)

o کاربرد: مقایسه دو گروه وابسته با داده های غیرنرمال یا ترتیبی.

o مثال: مقایسه سطح اضطراب دانشجویان (مقیاس ۱ تا ۵) قبل و بعد از کارگاه.

o نکته: ناپارامتری و برای داده های جفت شده.

7. آزمون کروسکال-والیس (Kruskal-Wallis)

o کاربرد: مقایسه بیش از دو گروه مستقل با داده های غیرنرمال یا ترتیبی.

o مثال: مقایسه رضایت مشتریان (مقیاس ۱ تا ۱۰) از سه رستوران.

o نکته: ناپارامتری و جایگزین ANOVA برای داده های غیرنرمال.

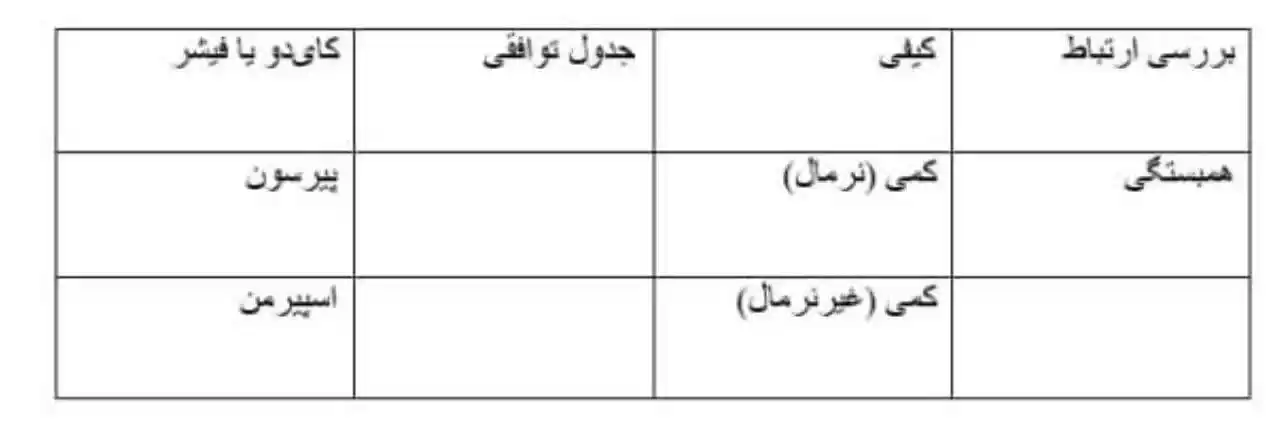
۳. آزمون های بررسی ارتباط

8. آزمون کای دو استقلال (Chi-Square Test of Independence)

o کاربرد: بررسی ارتباط بین دو متغیر کیفی در جدول توافقی.

o مثال: بررسی ارتباط جنسیت (مرد/زن) با ترجیح برند گوشی (اپل/سامسونگ).

o نکته: فرکانس مورد انتظار هر خانه باید حداقل ۵ باشه، وگرنه از فیشر استفاده کن.

9. آزمون فیشر (Fisher’s Exact Test)

o کاربرد: بررسی ارتباط دو متغیر کیفی در جدول توافقی با نمونه کوچک یا فرکانس کم.

o مثال: بررسی ارتباط نوع دارو (A/B) با بهبود بیماری (بله/خیر) در ۲۰ بیمار.

o نکته: برای جدول های ۲×۲ با فرکانس مورد انتظار زیر ۵ مناسبه.

10. آزمون مک نمار (McNemar Test)

o کاربرد: مقایسه داده های کیفی وابسته (مثل بله/خیر) در دو زمان یا شرایط.

o مثال: بررسی اینکه آیا ۳۰ بیمار بعد از درمان از «درد» به «بدون درد» تغییر کردن یا نه.

o نکته: برای جدول های ۲×۲ کیفی وابسته مناسبه.

11. آزمون کای دو خیر نیکوئی برازش (Chi-Square Goodness-of-Fit)

o کاربرد: بررسی تطابق توزیع یه متغیر کیفی با الگوی مورد انتظار.

o مثال: بررسی اینکه آیا توزیع رنگ ماشین ها (قرمز/آبی/سفید) تصادفیه (هر رنگ ۳۳٪).

o نکته: فرکانس مورد انتظار هر دسته باید حداقل ۵ باشه.

۴. آزمون های بررسی همبستگی

12. ضریب همبستگی پیرسون (Pearson Correlation)

o کاربرد: بررسی رابطه خطی بین دو متغیر کمی نرمال.

o مثال: بررسی رابطه بین ساعات مطالعه و نمره امتحان.

o نکته: داده ها باید نرمال و رابطه خطی باشه.

13. ضریب همبستگی اسپیرمن (Spearman Correlation)

o کاربرد: بررسی رابطه بین دو متغیر کمی غیرنرمال یا ترتیبی.

o مثال: بررسی رابطه بین رتبه تحصیلی و رضایت شغلی (مقیاس ۱ تا ۵).

o نکته: ناپارامتری و برای داده های رتبه ای مناسبه.

۵. آزمون های بررسی توزیع

14. آزمون کولموگوروف-اسمیرنوف (Kolmogorov-Smirnov)

o کاربرد: بررسی تطابق توزیع داده های کمی با یه توزیع خاص (مثل نرمال).

o مثال: بررسی اینکه آیا نمرات امتحان ۱۰۰ دانشجو نرماله یا نه.

o نکته: برای نمونه های بزرگ تر مناسبه.

15. آزمون شاپیرو-ویلک (Shapiro-Wilk)

o کاربرد: بررسی نرمال بودن داده های کمی.

o مثال: بررسی اینکه آیا زمان واکنش ۳۰ راننده نرماله یا نه.

o نکته: برای نمونه های کوچک (زیر ۵۰) دقیق تره.

۶. آزمون های پیشرفته تر

16. رگرسیون چندگانه (Multiple Regression)

o کاربرد: پیش بینی یه متغیر کمی با چند متغیر مستقل.

o مثال: پیش بینی فشارخون بر اساس سن، وزن، و ساعات ورزش.

o نکته: داده های وابسته باید نرمال باشن.

17. مدل های لجستیک (Logistic Regression)

o کاربرد: پیش بینی یه متغیر کیفی دوحالته (مثل بله/خیر).

o مثال: پیش بینی ابتلا به دیابت (بله/خیر) بر اساس سن و BMI.

o نکته: برای متغیرهای وابسته کیفی مناسبه.

18. مدل های مختلط (Mixed Models)

o کاربرد: تحلیل داده های طولی یا چندسطحی با اثرهای ثابت و تصادفی.

o مثال: بررسی نمرات دانش آموزان در سه سال با در نظر گرفتن اثر مدرسه.

o نکته: برای داده های وابسته و پیچیده مناسبه.

19. GEE (Generalized Estimating Equations)

o کاربرد: تحلیل داده های طولی با متغیر وابسته غیرنرمال یا کیفی.

o مثال: بررسی سطح استرس (کم/متوسط/زیاد) کارکنان در ۶ ماه با اثر ساعات کاری.

o نکته: برای داده های وابسته و غیرنرمال انعطاف پذیره.

مثال های کاربردی

مثال ۱: می خواهید بررسی کنید آیا میانگین فشارخون بیماران قبل و بعد از مصرف دارو تغییر کرده است.

- نوع داده: کمی (فشارخون)، وابسته (قبل و بعد).

- هدف: مقایسه دو گروه وابسته.

- آزمون: اگر داده ها نرمال باشند، آزمون تی جفت شده؛ اگر غیرنرمال، آزمون ویلکاکسون.

مثال ۲: می خواهید بررسی کنید آیا جنسیت بر انتخاب رشته تحصیلی تاثیر دارد.

- نوع داده: کیفی (جنسیت و رشته).

- هدف: بررسی ارتباط.

- آزمون: کای دو.

مثال ۳: می خواهید رابطه بین ساعات مطالعه و نمره امتحان را بررسی کنید.

- نوع داده: کمی (ساعات و نمره).

- هدف: همبستگی.

- آزمون: اگر نرمال، پیرسون؛ اگر غیرنرمال، اسپیرمن.

نوشته شده توسط : زهرا رازقی فر

razeghifarz@gmail.com

کانال یوتیوب من در حوزه هوش مصنوعی

https://www.youtube.com/@AIJourneyir